AI Material Model for LS-Dyna

The first open-source data-driven constitutive model for explicit finite element analysis.
Licenced under GPL v3 by the University of Oxford.

Free download from Github

Imagine modelling a whole turbine engine

Accounting for rate dependency, ageing, temperature gradients or engineered microsctructures increase the fidelity but also increase simulations’ cost and complexity. In other words, modelling anything beyond elasticity is tough!

WebSlides Files

Visualisation won’t be simple either

Post-processing large engineering simulations is transforms data into insight. The danger is that important information go missing if the visualisation is a barrier rather than a solution. Dedicated tools existing but are, as of today, rather difficult to grasp.

Motivations driving us

  • Need for a data-driven model

    Can we formulate an AI-based constitute model for finite element simulations?

  • Enhance visualisation

    Can we make use of virtual reality (VR) to improve post-processing of large simulations?

The AI Material Modelling project is a feasibility study that tries to bring new simulation tools to engineering students and researchers. The aim is to make our research more accessible, fun to learn and impactful.

You will need

On a Windows 10 PC, you can replicate our results with these software. There may be restrictions on your campus licenses, but even with the free student tear offered you should be able to follow along.

Let’s get started

Download the source code

git clone https://github.com/MattiaMontanari/ai-material-model.git

Inside the src directory there are three main folders to take a look at.

  • D1

    Data generation and ANN training workflow for elasticity

  • D2

    ANN for plastic user-defined materials

  • D3

    VR visualiser of D3Plot files

D1 - Data generation and network training

Generation of training data for a neural network that represents linear elastic isotropic material behaviour. Two neural networks are trained based on the generated data. One representing the normal stress response and the second one representing the shear stress response.

To get started run the following script

matlab WF_artificialData.m

This will:

  1. Generate and plot synthetic data
  2. Train the ANN for normal stress
  3. Train the ANN for shear stress


The output are the weights in Fortran format stored into weightsNormal.txt and weightsShear.txt.

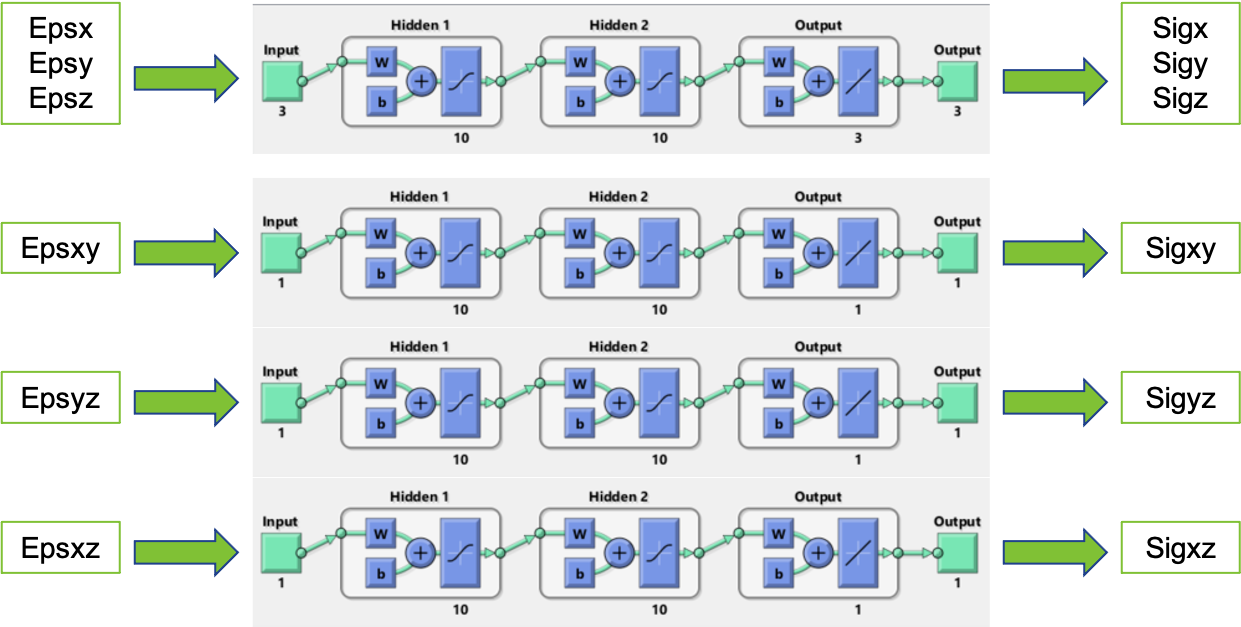
ANN architecture

A step by step guide and more insight on the ANN’s architecture are provided in the Matlab LiveScript WF_elasticData.mlx. As we are creating a simple constitutive model, the ANN has to relate strains to stresses. Normal loads are coupled into a unique network but the shear ones are not. The architecture is therefore pretty simple:

Cat

The output of the LiveScript can by downloaded from here if you have any issue running this first part.

Demonstration in LS-DYNA

Simple clamped cantilever with off axis displacement load problem is solved with the provided usermat umat47v.f. Please refer to LS-Dyna documentation to compile this usermat. The point load is actually applied to a corner element, for more information please inspect the provided input file cantilever2.key.

Note The usermat needs to be compiled jointly with the two weight text files that are produced after the ANN training.

Cat

Demonstration in LS-DYNA

As espcted, the ANN trained with synthetic data (obeying Hook’s law) matches well the stress distribution of an explity finite element simulation limited to Hook’s law.
This is an expected result which gives some confidence in the method.

Cat
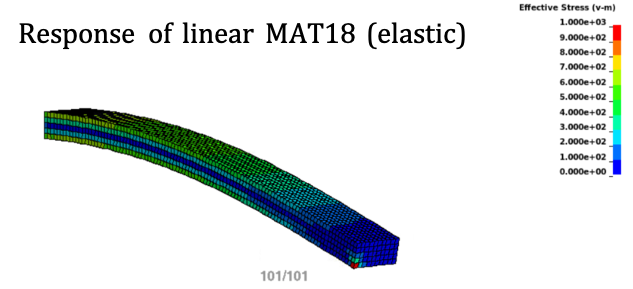
Built-in LS-Dyna MAT 18 stress response.

Cat
New ANN usermat stress response.

Take a break and see the bigger picture

In the next slide, 4 minutes from the TEDxCentraleNantes talk delivered by an inspiring Prof. Paco Chinesta on data-driven models.

D2 - Workflow for modelling plasticity

In this part we will use ANN for isotropic plastic material and compare against LS-Dyna’s MAT 018: a renown isotropic plasticity model with rate effects which uses a power law hardening rule.

Alike in the D1 part, we will take three steps:

  1. Generate data
  2. Training for plasticity
  3. Compare ANN usermat Vs. MAT 018

For linear plasticity brings the material response is path dependent and the data needs to be generated in finite element environment.

Generate data for plasticity

Compared to the priovious part D1, the generation of data for platicity is more involved. We could use experimental data, numerical data or a compbination of these. We are limited to numerical data as significantly easier to reduce, generate and mine.

We are going to use a bespoke single element library to generate the dataset representing plasticity. Such library consists of a large number of single element simulations loaded in many different ways. The aim is to span the whole space of loading conditions and train the ANN on this complete dataset.

L O A D I N G S

Training for plasticity

The Matlab script trainANN.m is provided, with a LiveScript, to show the training. As before, a list of weights in Fortran format is exported as result. An example has been placed into the 01_Compile subdir of 03_TestNetwork. These and the usermats provided can be compiled to run the two examples provided: cantilever and plate impact.

  • Need help generating data?

    Documenting all steps on any platform is not something we could possibly deliver at this stage, however we welcome questions and requests for support on the Github issue tracker. Alternatively you can reach the developers at the OXR Hub.

Demonstration in LS-DYNA

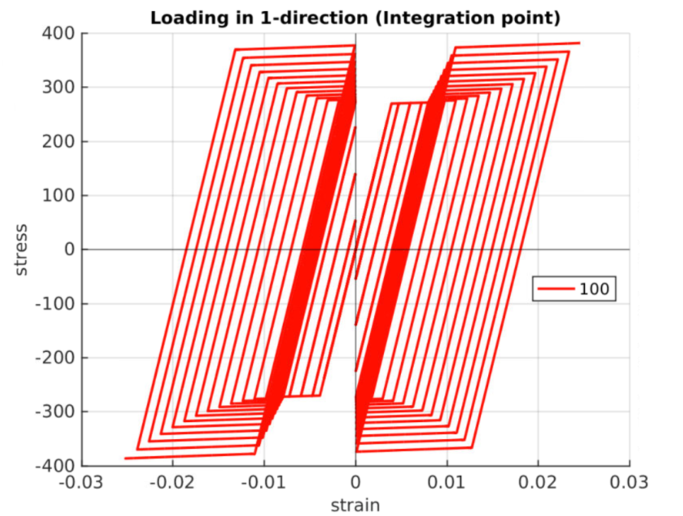
Comparison of cyclic load performance of MAT 018 (left) and usermat with ANN (right). As expected, these show similar stress response. These figures show results for strain rate 100.

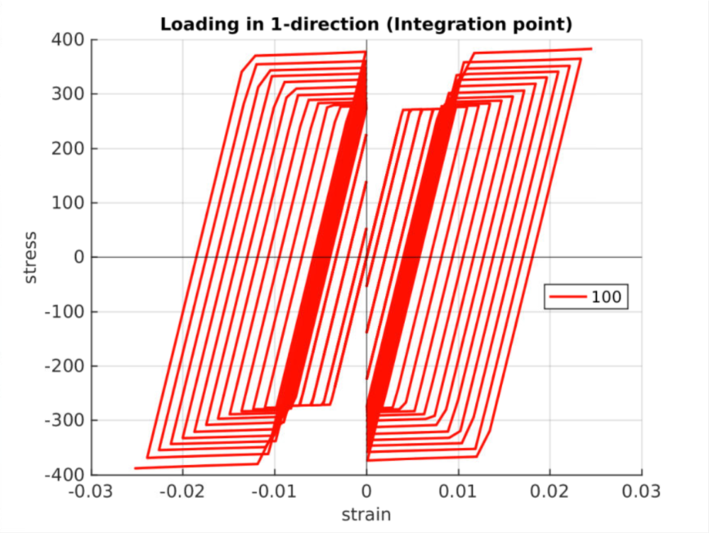
Demonstration in LS-DYNA

Comparison of of MAT 018 (top) and usermat with ANN (bottom). The figures on the left show nearly identical plastic strain and the figures on the right show stress values. The ANN model differes in the off-axis stres evaluation but remains overall very close to the repose of MAT 018.

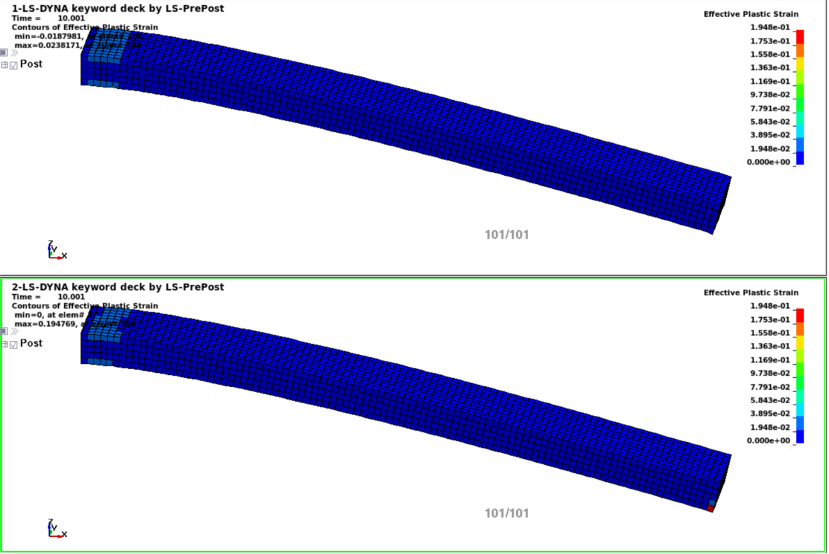
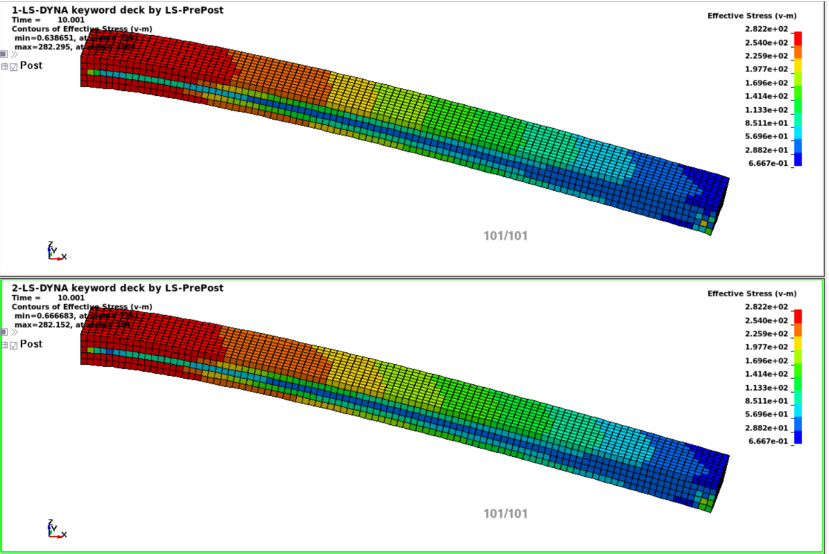
Demonstration in LS-DYNA

A rigid sphere impacting a deformable plate is the last validation test which will compare MAT 018 with the ANN usermat. On the right the animation of the test case and on the right the reaction force measues at the supports of the plate. Given the nature of the explicit finite element approximation, the discripancy between the models is somewhat acceptable - leaving room for further studies. What certain stands out in the response comparison is the good match between the solutions at the rebound impact.

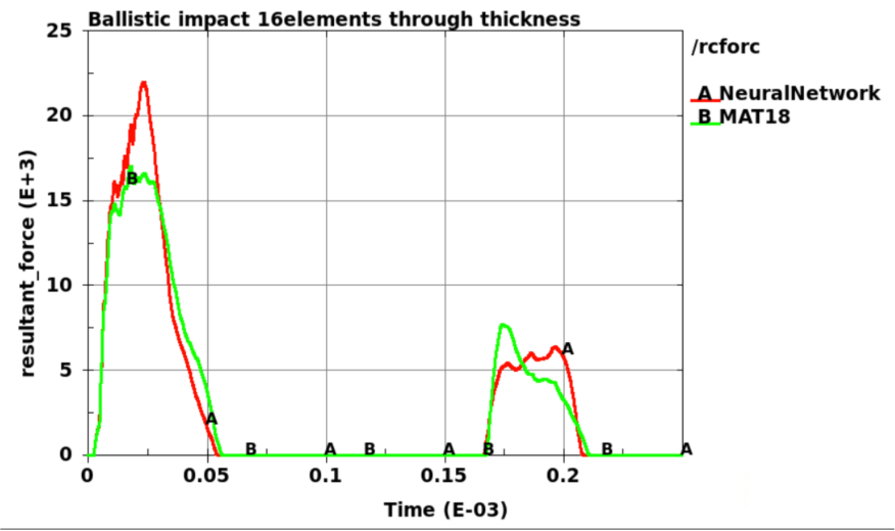
Dive deep into neural networks for dynamical systems

In the next slide, Prof. Nathan Kunts gives a hands-on-code lecture that will help you understanding more general concepts. Although not for finite element, the time map for the Lorenz problem will be very useful to create future ANN architectures for dynamic engineering simulations.

Get ready for VR

Simply launch Unity and enter VR with   this sample files

Next steps

As you have seen, the VR interface can load LS-Dyna outputs: the D3Plot files.
A sample can by downloaded from this link but you can also load your own D3Plots.

The VR interface is capable of rendering thousends of elements really quick, however is currently limited to tetrahedral elements only (elform 10 and elform 13). The code is available and if you want to expand it, it’s relatively simple to exted it to other forms - and pull requests are welcome of course!

More development information on the interface can be obtained from:

Acknowledgment

Thank you and thanks to the sponsoring partners of the Oxford-Singapore Human Machine collaboration from the MPLS Divsion, Oxford University.

Results computed with on the AWS cloud.